电阻的温度系数之统计算法

danioy

尝试用统计的算法测试几种常见电阻的温度系数。

3609曰： R = Rref X (1 + Alfa X ( T - T ref))

为了数据采集的方便，我们假定 Tref = 0 摄氏度。那么我们需要得到的就是一个阻值相对于温度的线性回归公式， R = R0 + Alfa T.

测试仪器： HP 3478   ( 没有用 6871 是因为昨晚没搞定 6871 的 GPIB 读数）

首先上阵的是 三环牌RTL 碳膜绿袍电阻一只，标称功率 0.25W 标称值 37.5KR1, 生产日期： 66.9

37.5K 绿袍电阻时间曲线

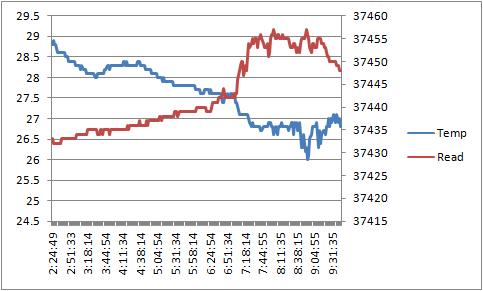
如果用电阻在26度和 29度附近的特征平均值直接计算， 该绿袍的温度系数大约 -231.543ppm/C

37.5K 绿袍线性回归分析

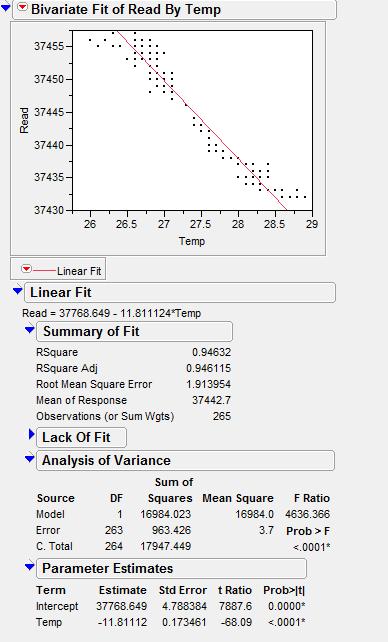
这样我们得出阻值相对于温度的线性回归公式： R=37768.649 - 11.811124 * T.
R^2 = 0.94632 也就是说94%的阻值变化可以用温度的变化来解释。

而且从这个线性公式，我们可以推导出该电阻的温度系数为-312.7229677ppm/C.


由于样本的温度范围很小，所以统计数显示出很好的线性。现在换成老大的数学模型，再来做一次统计分析：

老大曰： R/R20 = 1 + Alfa * (T - T20) + Beta * ( T-T20)^2

37.5K 绿袍老大的模型

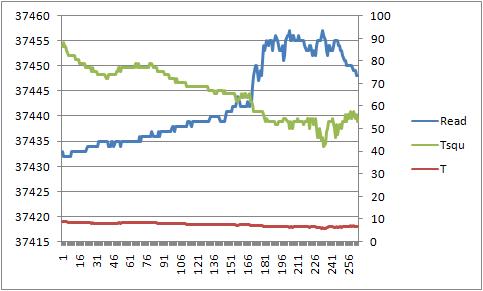
37.5K 绿袍老大的模型分析

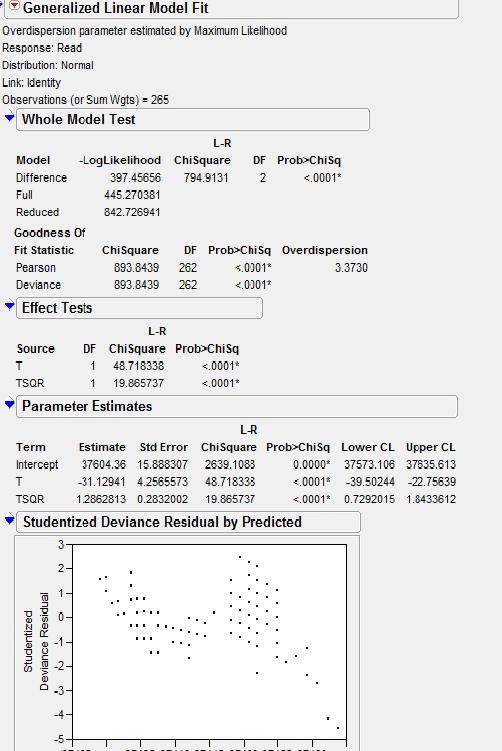
结果也是显性的。

R = 37604.36 - 31.12941 T + 1.2862813 T^2

则 温度系数为： - 827.8 ppm/C

yjm2000

一般的电阻温度系数不是线性的吧？

danioy

引用第1楼yjm2000于2009-05-10 13:07发表的  :
一般的电阻温度系数不是线性的吧？

取决于数学模型的选择 和验证。

lymex

第一个图形正确、结果也正确。第2个图形结果看来有误。
按照第一个直线模型，应该是斜率=-11.8，温度系数为-315ppm/C


补充：
Alpha系数是与温度有关的，如果是线性模型，是假设无关的，但只能适合一个小的范围
如果用了2次模型，那么基准温度选择的比实际温度差别大，误差就大了。

换句话说，第2种算法也正确，但得到的Alpha温度系数是20度下的。

danioy

为什么两个数学模型得出的值相差3倍之多？

在老大的指导下，我们重新做一次第二种模型的运算，唯一的区别是：

第一楼的参考温度点是 20度，我们现在把参考温度点设置为取样温度的中间数：27.5度，二次回归的结果：

37.K绿袍二次回归参考27,5度

统计分析同样是显性的，但alpha 降到了 11.5左右。从而 27.5度温飘大约： -309ppm/C.

结论： 在不同温度点，温飘不同；

lymex

看来RTL电阻温度系数还是很大